Manipulador RR y simulación con MATLAB

ANÁLISIS CINEMÁTICO DEL MANIPULADOR RR
Y SIMULACIÓN CON MATLAB

ROBÓTICA

Introducción a MatLab

MatLab es un lenguaje de programación interpretado en el que las variables son matrices y, por tanto, las operaciones básicas aritméticas y lógicas son operaciones matriciales. Esto hace que MatLab sea una herramienta muy adecuada para cálculo matricial y, en concreto, para simulación de robots.

A continuación se muestran algunos ejemplos de operaciones con MatLab:

Asignación de valores a vectores y matrices:

Para las columnas se utiliza el espacio en blanco como separador y el punto y coma para las filas.

Productos matriciales y escalares:

El primer producto representa la operación de transformar el vector x con la matriz A. El segundo es el producto escalar de x por y, donde x, representa el vector x traspuesto. El tercer producto tiene como resultado un vector w en el que cada componente se obtiene multiplicando las componentes las componentes correspondientes de x e y.

Pueden extraerse submatrices o elementos de una matriz:

A(0,3)
A(2:3,1:3)
A(2:3,:)
A(:,1)

Funciones y gráficas: las funciones también se manejan vectorialmente. Por ejemplo, para generar y dibujar la función sin(t), podemos ejecutar:

t=[0:0.01:2]*pi;
y=sin(t);
plot(t,y) La primera instrucción genera un vector con los valores de la variable independiente t desde 0 a

con incrementos de 0.01. El segundo comando genera el vector correspondiente con los valores de la función, y el tercero dibuja la gráfica de y en función de t. Los ";" evitan que el resultado de cada instrucción sea mostrado por pantalla (sólo útil en comandos que produzcan resultados numéricos).

Problema Cinemático Directo

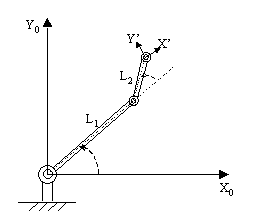
Como ya se ha indicado, Matlab es una herramienta apropiada para el análisis y simulación de problemas robóticos. Por ejemplo, para dibujar 21 puntos de la trayectoria que recorre el ET de un manipulador RIR (con enlaces de longitud L₁=L₂=1) cuando las dos variables rotacionales q₁yq₂ varían uniformemente de 0 a , habría que ejecutar los siguientes comandos:

Ll=l;
L2=1;
thl=0:(pi/2)/20:pi/2;
th2=0:(pi/2)/20:pi/2;
px=Ll*cos(thl)+L2*cos(thl+th2)
py=Ll*sin(thl)+L2*sin(thl+th2)
plot(pX'PY)

Las dos primeras instrucciones asignan a las longitudes de los enlaces L_l=l y L₂=1. Las dos siguientes instrucciones generan dos vectores, th1 y th2, que contienen todos los valores de los ángulos entre q₁ y q₂ que varían uniformemente de 0 a a intervalos regulares de por lo que se han tomado un total de 21 puntos de la trayectoria.

Posteriormente, se ha hecho uso de las ecuaciones cinemáticas del manipulador para obtener las 21 posiciones cartesianas (x,y) consecutivas. Las variables px y py son dos vectores que contienen los 21 valores de las coordenandas X e Y, respectivamente. El comando plot dibuja el vector de valores de la variable dependiente py en función del vector de valores de la variable independiente py.

Las instrucciones anteriores pueden ser incluidas en un fichero de texto con extensión *.m por ejemplo, practica2.m, y ejecutadas en la línea de comando de MatLab con el comando practica2 (sin extensión). Las distintas partes de la práctica pueden separarse mediante comandos pause que detienen la ejecución (hasta que se pulse una tecla). MatLab incorpora comandos operativos como dir, cd y path, que tienen el mismo significado que sus correspondientes en MS-DOS. Para obtener información sobre los comandos y funciones básicas de Matlab existe un manual "on line" accesible con el comando help.

Uso de funciones:

Cuando se va a hacer uso repetido de un conjunto de instrucciones, es conveniente escribir una función que las contenga. Así, podemos escribir una función que resuelva de forma genérica el problema cinemático directo de un robot RR de la siguiente manera:

donde p es la variable que se retorna, y pcd es el nombre de la función seguido de los argumentos (entre paréntesis). La variable p contiene en la primera fila la secuencia de coordenadas X, y en la segunda las Y. La función debe escribirse en un fichero de texto separado cuyo nombre debe ser el de la función seguido de la extensión .m (pcd.m en este caso).

Haciendo uso de la función anterior, la trayectoria anterior se trazaría mediante:

En este caso, el comando plot dibuja la segunda fila de la matriz p en función de la primera.

Gráfica de la configuración espacial del robot

En los ejemplos anteriores se ha dibujado exclusivamente la trayectoria descrita por el ET, pero no el robot. Dada una configuración espacial (por ejemplo, L₁=300 y L₂ = 600), puede obtenerse un gráfico del robot RR mediante:

donde robot es la función que dibuja el robot en pantalla. Para desarrollar esta función, debe tenerse en cuenta que el robot se compone de dos segmentos lineales: el primero entre los puntos (0,0) y (cosq₁, sinq₁), y el segundo entre este último punto y la posición del ET p = (px, py). Para trazar el robot, bastará con realizar un plot en el que la variable independiente y dependiente son dos vectores conteniendo las coordenadas X e Y, respectivamente, de los tres puntos mencionados. Una posible implementación de la función es la siguiente:

El comando axis asegura que en sucesivos plot´s se conservan los rangos X e Y de la gráfica.

Trazado de la trayectoria:

En este apartado, se desarrollará un programa.m que simule el movimiento del robot y trace la trayectoria correspondiente del ET cuando las variables de articulación q ₁y q₂,varían uniformemente entre 0 y

. Para ello, debe calcularse el robot y la posicion del ET en una serie de puntos. Esto puede hacerse con un programa basado en un bucle for, conteniendo la representación desarrollada en el apartado anterior, con la siguiente estructura:

Npuntos=10;
for n=0 : Npuntos
    thl=(Pi/2)*n/Npuntos;
    th2=(p¡/2)*n/Npuntos;
    ... (a completar)
    pause
    clf
end

En cada punto debe dibujarse el robot en la posición actual y la trayectoria desarrollada hasta ese momento (a modo de "rastro"). Para dibujar la trayectoria pueden ir acumulándose en una matriz de dos filas los puntos ya recorridos de la trayectoria:

En cada punto de la trayectoria hay que actualizar esta matriz, añadiéndole una nueva columna con el nuevo punto de la trayectoria. Esto puede hacerse con una instrucción del tipo pxy=[pxy pact]; donde pxy contiene los puntos ya recorridos, y pact el punto actual.

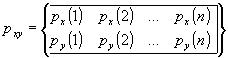
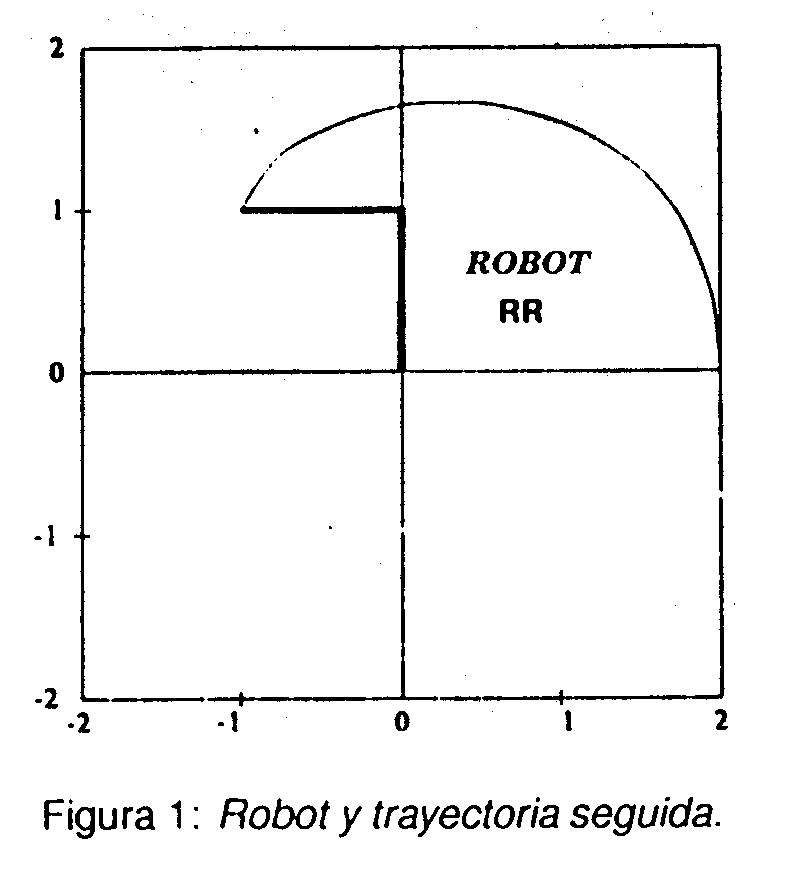
Para su realización, debe tenerse en cuenta que MatLab tiene disponibles instrucciones de control de flujo similares a las del lenguaje C (if-else-end y while-end). Además, para simular el movimiento pueden usarse los comandos pause (detiene la ejecución hasta que se pulsa una tecla), cif (borra el contenido de un gráfico sin eliminar la ventana correspondiente), y hold on y hold off, que permiten añadir una curva en un gráfico ya creado anteriormente (esto permite superponer la gráfica de la trayectoria a la del robot). Al final de la trayectoria, la ventana de simulación debería presentar el gráfico indicado en la figura 1

Problema Cinemático Inverso

Normalmente las trayectorias se expresan en coordenadas cartesianas que deben ser traducidas a variables de articulación. Esto es lo que se conoce como problema cinemático inverso. Las ecuaciones correspondiente para el robot RR son:

(1)

Por ejemplo, una trayectoria rectilínea entre dos puntos cualesquiera (x₁, y₁) y (x₂, y₂) tiene la siguiente expresión:

Escribir un programa que simule el movimiento del robot y dibuje la trayectoria (similar al realizado en el apartado anterior) para un movimiento rectilíneo entre dos puntos cualesquiera. Para ello, se utilizará la función robot de los apartados anteriores y se construirá una nueva función pci que implemente las ecuaciones (1). Debe tenerse en cuenta que las funciones acos (arco coseno) y atan (arco tangente) de Matlab toman valores en los intervalos [o,] y [-,], respectivamente.

Con este programa se probarán las siguientes trayectorias:

(x₁, y₁)=(2, 0), (x₂, y₂)=(0, 2).
(x₁, y₁)=(1, 1), (x₂, y₂)=(-1, 0). Diagnosticar los posibles problemas de continuidad y corregir la función pci para solventarlos. Para ello, debe tenerse en cuenta que la función atan no determina correctamente el cuadrante del ángulo solución, por lo que debe sustituirse por la función atan2.
(x₁, y₁)=(1, 0), (x₂, y₂)=(-1, 0). Diagnosticar los posibles problemas de continuidad y corregir la función pci para solventarlos. Para ello, debe tenerse en cuenta que la función acos tiene, en realidad, dos soluciones para q₂: el ángulo positivo que devuelve MatLab, y el mismo valor, pero negativo. Para escoger una solución u otra, puede tomarse el siguiente criterio: dado que q₁ se obtiene a partir de q₂, es lógico seleccionar la solución de acos(q₂) que hace que el incremento en q₁ desde el punto anterior de la trayectoria al actual sea el menor posible.

Finalmente, se dibujarán las funciones temporales de las variables de articulación q₁ =q₁(n) y q₂=q₂(n), donde n representa el instante de muestreo temporal.

Última actualización 3 Abril de 2000