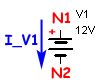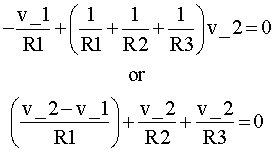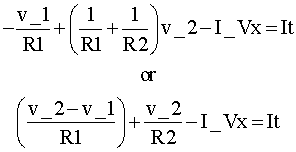SCAM no puede leer directamente un fichero de esquemático convencional, por ello se ha desarrollado un filtro importador de Descripcion de nodos con un formato similar al utilizado por SPICE. Si has utilizado anteriormenteSPICE (Simulation Program with Integrated Circuit Emphasis) estarás familiarizado con los ficheros de descripción de circuitos .cir. Un buen ejemplo está disponible en la WEBde Jan Van Der Spiegel en la University of Pennsylvania. El proceso anterior se describe a continuación..
Definamos un fichero o netlist del circuito divisor con carga mostrado:
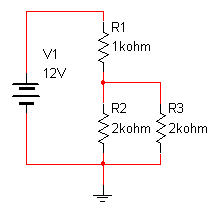
Como primera tarea se deben definir los números asociados a los diferentes nodos. El nodo de referencia debe numerarse como 0 y tras esto y de manera consecutiva el resto de nodos del circuito.
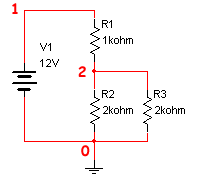
SCAM necesita un fichero de texto donde en cada línea de texto aparece un componente del circuito. Este circuito tiene 4 componentes (3 resistencias y una fuente de tensión) y necesitará 6 líneas de texto para su definición. Cada tipo de componente tiene su propio formato de descripción. Éstos son los siguientes. Las etiquetas N1, N2, etc... corresponden a los nodos del circuito to the nodes in the circuit.
| Componente | Símbolo | Descripción |
| Resistencia | 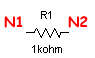 |
R1 N1 N2 1000
|
| Condensador | 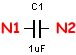 |
C1 N1 N2 1E-6
|
| Inductancia | L1 N1 N2 1E-3
| |
| Fuente de Tensión | 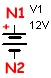 |
V1 N1 N2 12
|
| Fuente de Corriente | 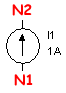 |
I1 N1 N2 1
|
| Amplificador Operacional | 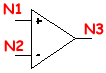 |
O1 N1 N2 N3
|
Se va a definir la correinte que atravies la fuente de tensión para finalizar el esquema del Circuito:
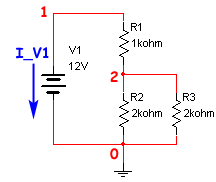
EL fichero de nodos o netlist es:
V1 1 0 12 R1 1 2 1000 R2 2 0 2000 R3 2 0 2000 |
Ejemplo 1: Tensiones
El circuito que se va a analizar es:
Se debe crear el netlist :
y almacenarlo en un directorio accesible por MatLab®. El fichero se ha editado (usando el editor de MatLab® ) y almacenado en el directorio SCAM como Example1.cir. Si en estos momentos estas ejecutando MatLab®, deberías obtener esta salida al ejecutar el comando dir:
>> dir . .. scam.asv scam.m Example1.cirAntes de ejecutar SCAM es necesario definir una variable global que contenga el nombre del fichero a analizar en la variable fname y posteriormente ejecutar el programa. La salida de la ventana de ejecución de MatLab® quedaría:
>> fname='Example1.cir'; >> scam Started -- please be patient. Done! Elapsed time = 0.651 seconds. Netlist V1 1 0 12 R1 1 2 1000 R2 2 0 2000 R3 2 0 2000 Solved variables: [ v_1] [ v_2] [ I_V1]Se muestra el netlist seguido de las incógnitas del circuito que se van a obtener. Veamos el valor de la tensión en el nodo 2 ( v_2):
>> v_2
v_2 = 1/(R2*R3+R1*R3+R1*R2)*R2*R3*V1o I_V1 (la corriente que atraviesa la fuente de tensión)
>> I_V1
I_V1 = (-R3-R2)/(R2*R3+R1*R3+R1*R2)*V1Además de las incógnitas, se crean varias variables adicionales en el espacio de trabajo o workspace (esta es la razón por la que SCAM no es una función sino un script). Además de las variables se crean las equituetas correspondientes a los valores de los componentes. Se puede examinar el valor de cualquier elementolemento, por ejemplo V1 o R2
>> V1
V1 = 12
>> R1
R1 = 1000Se pueden utilizar estos valores para obtener resultados numéricos de las incógnitas:
>> eval(v_2)
ans = 6
>> eval(I_V1)
ans = -0.0060que muestran que la tensión en el nodo 2 es de 6 voltios y la corriente a través de V1 es de 6 mA.
Ejemplo 2: Corrientes
Si estamos interesados en la corriente que circula por R2 podemos obtener la solución tanto numérica como simbólica:
>> v_2/R2
ans = 1/2000/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.0030La corriente a través de R1, desde el nodo1 al 2, es el cociente de la tensión en los extremos de R1 y su valor.
>> (v_1-v_2)/R1
ans = 1/1000*V1-1/1000/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.0060Otros parámetros pueden obtenerse de forma similar, como por ejempo el ratio entre v_2 y V1:
>> v_2/V1
ans = 1/12/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.5000
Ejemplo 3: Obtención de las Ecuaciones del Análisis Nodal Modificado
SCAM utiliza la definición generalizada del método MNA y por lo tanto trabaja con las matrices A, X y Z (SCAM utliza las variables X y Z en mayúsculas).
>> A
A = [ 1/R1, -1/R1, 1]
[ -1/R1, 1/R1+1/R2+1/R3, 0]
[ 1, 0, 0]
>> X
X = [ v_1]
[ v_2]
[ I_V1]
>> Z
Z = [ 0]
[ 0]
[ V1]Se pueden utilizar estas variables para obtener las ecuaciones del circuito. Para obtener la parte izquierda de las ecuaciones únicamente es necesario realizar A*X:
>> A*X ans = [ 1/R1*v_1-1/R1*v_2+I_V1] [ -1/R1*v_1+(1/R1+1/R2+1/R3)*v_2] [ v_1]y con un mejor aspecto:
>> pretty(A*X) [ v_1 v_2 ] [ --- - --- + I_V1 ] [ R1 R1 ] [ ] [ v_1 / 1 1 1 \ ] [- --- + |---- + ---- + ----| v_2] [ R1 \ R1 R2 R3 / ] [ ] [ v_1 ]La parte derecha de la ecuación viene especificada por Z:
Z = [ 0] [ 0] [ V1]Utilizando la información anterior, se pueden obtener las ecuaciones MNA. Para obtener las ecuaciones para el nodo 2, se toma la segunda fila con la parte izquierda y derecha de las ecuaciones:
Ejemplo 4: Un circuito algo más complejo
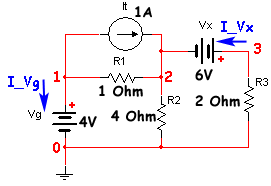
Este script se puede utilizar para circuitos más complejos como el siguiente (Ejemplo 3 de la Página de Ejmeplos del Análisis MNA con valores concretos para cada componente) (con todos los nodos numerados y definidas las tensiones y corrientes de cada fuente):
El netlist para el circuito es el siguiente:
Este netlist se ha almacenado en un fichero Ejemplo4.cir. Para analizar el circuito se debe realizar lo siguiente:
>> fname='Example4.cir'; >> scam Started -- please be patient. Done! Elapsed time = 2.544 seconds. Netlist Vg 1 0 4 Vx 3 2 6 R1 1 2 1 R2 2 0 4 R3 3 0 2 It 1 2 1 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vg] [ I_Vx]Se puede obtener la tensión del nodo 2 de manera simbólica o numérica:
>> v_2 v_2 = R2*(It*R1*R3+Vg*R3-Vx*R1)/(R2*R3+R1*R3+R1*R2) >> eval(v_2) ans = 1.1429La corriente que circula por R1 (simbólica o numérciamente):
>> (v_1-v_2)/R1 ans = Vg-R2*(It*R1*R3+Vg*R3-Vx*R1)/(R2*R3+R1*R3+R1*R2) >> eval(ans) ans = 2.8571La ecuación MNA para el nodo 2:
>> q=A*X q = [ 1/R1*v_1-1/R1*v_2+I_Vg] [ -1/R1*v_1+(1/R1+1/R2)*v_2-I_Vx] [ 1/R3*v_3+I_Vx] [ v_1] [ -v_2+v_3] >> pretty(q(2)) v_1 / 1 1 \ - --- + |---- + ----| v_2 - I_Vx R1 \ R1 R2 / >> Z(2) ans = Ito de una manera más clara:
Ejemplo 5: Amplificadores Operacionales con resistencias
El próximo ejemplo muestra un circuito con un amplificador operacional con 2 resisitencias en la configuración clásica de inversor y con el netlist (Ejemplo5.cir).
Circuito Netlist
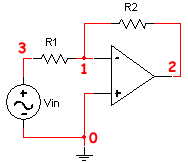
Ya que no se disponen de valores para los componentes del circuito, se utilizará la etiqueta "Symbolic". Ahora se puede analizar el circuito y determinar la ganancia de tensión entre Vin y el nodo 2.
>> fname='Example5.cir'; >> scam Started -- please be patient. Done! Elapsed time = 1.633 seconds. Netlist Vin 3 0 Symbolic R1 1 3 Symbolic R2 2 1 Symbolic OAmp 0 1 2 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vin] [ I_OAmp] >> v_2/Vin ans = -1/R1*R2Algunas notas de interés del circuito:
- Si un valor no se asocia a un elemento, el valor puede ser declarado simbólico. Sin embargo ésto no es necesario, basta con no incluir un número sino una referencoa como "xyz" o dejarlo en blanco.
- Dado el modo en el que el análisis MNA utiliza los amplificadores operacionales, el circuito anterior el resultado será independiente de la polaridad de entrada del amplificador operacional. Ya sabemos que en la práctica esto no es posible. Es responsabilidad del usuario asegurar la realimentación positiva en el Operacional.
Ejemplo 6: Convertir la función de transferencia simbólica en un objeto MatLab®.
Muy a menudo utilizamos MatLab® para realizar cálculos y simulaciones sobre todo cuando trabajamos con funciones de transferencia. Este circuito se ha extrahido de la página MNA de Condensadores e Inductores con valores para cada componentes. El netlist se facilita en el fichero Ejemplo6.cir.
Circuito Netlist
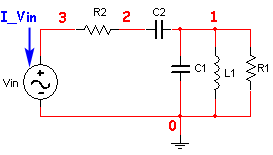
Se resuelve y se obtiene la función de transferencia simbólica:
>> fname='Example6.cir'; >> scam Started -- please be patient. Done! Elapsed time = 1.583 seconds. Netlist Vin 3 0 Symbolic R2 3 2 1000 R1 1 0 1000 C1 1 0 1E-6 C2 2 1 10E-6 L1 1 0 0.001 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vin] >> v_2/Vin %Find transfer function between input and node 2 ans = (s*L1+s^2*C1*R1*L1+s^2*C2*R1*L1+R1)/(s*L1+s^2*L1*C2*R2+s^2*C1*R1*L1+s^3*C1*R1*L1*C2*R2+s^2*C2*R1*L1+R1+R1*s*C2*R2) >> collect(ans) %Collect similar terms ans = ((C2*R1*L1+C1*R1*L1)*s^2+s*L1+R1)/(s^3*C1*R1*L1*C2*R2+(C2*R1*L1+L1*C2*R2+C1*R1*L1)*s^2+(L1+R1*C2*R2)*s+R1) >> pretty(ans) %Pretty print it 2 / 3 ((C2 R1 L1 + C1 R1 L1) s + s L1 + R1) / (s C1 R1 L1 C2 R2 / 2 + (C2 R1 L1 + L1 C2 R2 + C1 R1 L1) s + (L1 + R1 C2 R2) s + R1)
Se puede obtener el valor numérico de la función de transferencia:
>> eval(v_2/Vin) ans = (1/1000*s+11/1000000*s^2+1000)/(10001/1000*s+21/1000000*s^2+1/100000000*s^3+1000)
Aunque esta expresión es correcta, no se presenta en un formato conveniente y no se puede simular directamente. Sin embargo puede ser convertida a un objeto MatLab® de función de transferencia. Lo primero es separar el numerador y denominador y después convertirlos en polinomios MatLab®.
>> [n,d]=numden(eval(v_2/Vin))
n = 100000*s+1100*s^2+100000000000
d = 1000100000*s+2100*s^2+s^3+100000000000
>> mySys=tf(sym2poly(n),sym2poly(d))
Transfer function:
1100 s^2 + 100000 s + 1e011
--------------------------------
s^3 + 2100 s^2 + 1e009 s + 1e011
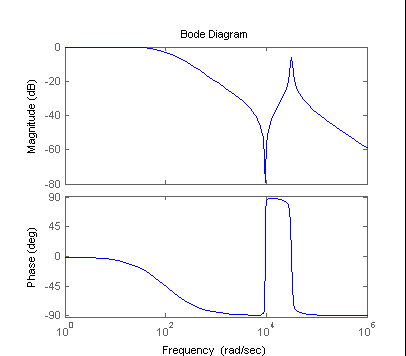
Y ahora ya se puede realizar gran cantidad de análisis entre ellos las del cálculo de respuesta al escalón y el Diagrma de Bode.
|
Respuesta al Escalón |
Diagrama de Bode |
| >> step(mySys) | >> bode(mySys) |
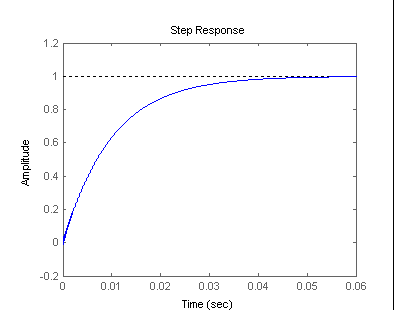 |
 |
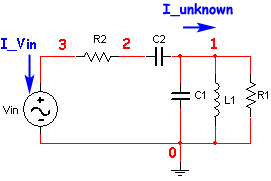
Ejemplo 7: Cálculo de la corriente en un conductor
En el siguiente circuito se plantea el cálculo de la corriente que circula por un conductor:
Para encontrar el valor de la corriente tendríamos varias alternativas:
- Por un lado, se podría estimar el balance de corientes que entran y salen del nodo 1
- O introducir una fuente de tensión nula que se comporta de manera similara un corto circuito y separ el nodo de interés. El netlist es Ejemplo7.cir.
Circuito Netlist
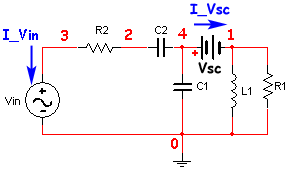
Esta fuente de tensión no tiene efecto sobre el comportamiento del circuito, pero fuerza el cálculo de la corriente I_Vsc:
>> fname='Example7.cir'; >> scam Started -- please be patient. Done! Elapsed time = 3.014 seconds. Netlist Vin 3 0 Symbolic R2 3 2 1000 R1 1 0 1000 C1 4 0 1E-6 C2 2 4 10E-6 L1 1 0 0.001 Vsc 4 1 0 Solved variables: [ v_1] [ v_2] [ v_3] [ v_4] [ I_Vin] [ I_Vsc] >> eval(I_Vsc) ans = -1/100000*(-1/1000*s-1000)*s*Vin/(10001/1000*s+21/1000000*s^2+1/100000000*s^3+1000) >> simplify(ans) ans = (s+1000000)*s*Vin/(1000100000*s+2100*s^2+s^3+100000000000) >> pretty(ans) (s + 1000000) s Vin ------------------------------------------ 2 3 1000100000 s + 2100 s + s + 100000000000